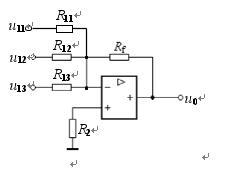
在集成电路设计中，集成运算放大器（简称运放）是构成各种模拟信号处理电路的核心元件。本文将以一个典型的由运放构成的运算电路为例，详细推导其输入输出之间的关系，并深入分析该电路所实现的运算功能。\n\n### 一、电路结构与基本假设\n\n假设电路为经典的反相比例运算电路或同相比例运算电路，这是两种最基础且应用最广泛的运放电路拓扑。为进行一般性分析，我们基于以下理想运放条件：\n1. 开环电压增益无穷大。\n2. 输入阻抗无穷大。\n3. 输出阻抗为零。\n4. 输入失调电压、输入偏置电流等非理想因素为零。\n\n### 二、输入输出关系推导\n\n以最典型的反相比例运算电路为例进行推导。该电路结构为：输入电压 \( V{in} \) 通过一个输入电阻 \( R1 \) 连接到运放的反相输入端（-）。运放的同相输入端（+）通过一个电阻 \( R3 \) 接地（通常 \( R3 \) 用于平衡偏置电流，其值等于 \( R1 \) 与反馈电阻 \( Rf \) 的并联值，但在理想分析中常直接接地）。在反相输入端与输出端 \( V{out} \) 之间连接有反馈电阻 \( Rf \)。\n\n根据理想运放“虚短”（两输入端电位相等）和“虚断”（流入两输入端的电流为零）的特性：\n1. 由于同相输入端接地，反相输入端电位也为零，即“虚地”。\n2. 流过电阻 \( R1 \) 的电流 \( I1 \) 全部流过反馈电阻 \( Rf \)，即 \( I1 = If \)。\n\n由此可得：\n\\[ I1 = \\frac{V{in} - 0}{R1} = \\frac{V{in}}{R1} \\]\n\\[ If = \\frac{0 - V{out}}{Rf} = -\\frac{V{out}}{Rf} \\]\n由于 \( I1 = If \)，因此：\n\\[ \\frac{V{in}}{R1} = -\\frac{V{out}}{Rf} \\]\n整理得到输入输出关系：\n\\[ V{out} = -\\left( \\frac{Rf}{R1} \\right) V{in} \\]\n\n对于同相比例运算电路（输入电压 \( V{in} \) 接同相端，反相端通过电阻 \( R1 \) 接地并通过 \( Rf \) 反馈至输出），采用类似的分析方法可得：\n\\[ V{out} = \\left( 1 + \\frac{Rf}{R1} \\right) V{in} \\]\n\n### 三、电路功能分析\n\n1. 数学运算功能：上述推导明确显示，这两种基本电路实现了输入电压 \( V{in} \) 与一个常系数（由外部电阻 \( R1 \) 和 \( Rf \) 的比值决定）的乘法运算。反相电路的系数为 \( -Rf/R1 \)，输出与输入反相；同相电路的系数为 \( 1 + Rf/R1 \)，输出与输入同相。通过选择不同的电阻值，可以灵活设置放大倍数（增益）或衰减系数。这是模拟计算机中进行比例、缩放等线性运算的基础单元。\n\n2. 信号调理功能：在更广泛的模拟信号处理系统中，此类电路是核心的放大器。通过精确设置电阻网络，可以设计出特定增益的电压放大器，用于将微弱的传感器信号（如热电偶、应变片、麦克风信号）放大到适合后续电路（如模数转换器ADC）处理的电平范围。其高输入阻抗和低输出阻抗特性也便于实现级联和阻抗匹配。\n\n3. 构建模块功能：此基本运算电路是构建更复杂功能电路的基石。通过增加更多的输入电阻，可以构成加法器（反相加法电路）。通过与电容组合，可以构成积分器或微分器，实现动态的微积分运算，广泛应用于波形生成、滤波器和控制系统。通过改变反馈网络的复杂程度（如引入非线性元件），还能实现对数、指数等非线性运算。\n\n4. 集成电路设计意义：在芯片设计层面，尽管基本运放本身是一个高度集成的器件，但其外围的电阻网络（\( R1, R_f \)）决定了电路的整体功能。在单片集成电路设计中，这些电阻可以通过晶圆上的薄膜电阻工艺精确实现，从而将整个运算功能（如可编程增益放大器PGA）集成到单一芯片中，实现系统的小型化、高可靠性和低成本批量生产。分析此类电路是理解模拟IP模块、数据转换器前端、滤波器和稳压器等复杂IC子系统工作原理的关键第一步。\n\n### 四、结论\n\n由集成运算放大器与电阻网络构成的基本运算电路，其核心功能是实现对输入电压的线性比例运算（放大或衰减）。反相与同相两种配置提供了增益符号和输入阻抗上的不同选择。该电路不仅是实现模拟数学运算的基础单元，更是现代电子系统中不可或缺的信号调理与放大模块。深入理解其输入输出关系及工作原理，是进行模拟集成电路与系统设计、分析和应用的重要基础。